OMSCS-ML课程笔记13-Markov Decision Processes

Created in October 30, 2021

2021   ·   CS7641-ML   ·   OMSCS

这个系列是Gatech OMSCS 机器学习课程(CS 7641: Machine Learning)的同步课程笔记。课程内容涉及监督学习、无监督学习和强化学习三个部分，本节开始介绍强化学习的相关内容。

强化学习(reinforcement learning)是机器学习的另一个重要组成部分。在强化学习任务中，我们希望智能体(agent)能够通过和环境的互动来学习到如何进行决策并获得最大收益。

Markov Decision Processes

强化学习的基本理论框架是马尔科夫决策过程(Markov decision processes, MDP)，这里首先介绍一些相关的概念：

  • 智能体自身的状态(state)用\(s\)来表示；
  • 智能体可以采取一些行为(action)来跟外界进行互动，用\(a\)来表示；
  • 当智能体执行了行为\(a\)后它自身的状态会发生改变，状态转移(transition)用\(T\)来表示\(T(s, a, s') = P(s' \vert s, a)\)；
  • 当智能体的状态发生转移时，外界环境会给予它一定的回报(reward)记为\(R\)。

我们假定系统满足马尔科夫性(Markovian property)，即状态转移仅与当前状态有关而与转移的历史无关；此外我们还默认环境是稳定的，它在和智能体的互动中不会发生改变。这样我们可以把智能体和环境的互动过程用下图来表示：

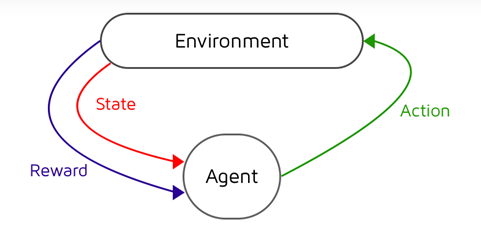
强化学习的目标是得到一个最优的策略(policy)使得智能体能够获得尽可能多的回报。所谓「策略」是指行为关于状态的函数\(\Pi(s): S \rightarrow A\)，它告诉智能体在给定的状态\(s\)下该如何确定自身的行为。在所有的策略中能够最大化回报的策略称为最优策略(optimal policy)，一般用\(\Pi^*\)来表示。

接下来的问题是如何衡量回报的大小。假设智能体的决策序列是无限的，我们需要引入一个折扣系数(discount factor)来计算回报序列的效用(utility)：

\[U(s_0, s_1, s_2, ...) = \sum_{t=0}^\infty \gamma^t R(s_t)\]

其中\(\gamma\)的取值范围是\(0 \lt \gamma \lt 1\)，\(\gamma\)越接近于0表示越关注于当前阶段的收益，\(\gamma\)越接近于1表示越关注于长远阶段的收益。引入折扣系数的主要目的是将效用转化为一个几何级数的计算，使得对于无限长的序列效用值仍然能够收敛：

\[\sum_{t=0}^\infty \gamma^t R(s_t) \leq \sum_{t=0}^\infty \gamma^t R_{\max} = \frac{R_{\max}}{1 - \gamma}\]

Bellman Equation

对于给定的策略\(\Pi\)，我们可以定义根据该策略在状态\(s\)下对应的效用为：

\[U^\Pi (s) = \mathbb{E} \bigg[ \sum_{t=0}^\infty \gamma^t R(s_t) \bigg\vert \Pi, s_0 = s \bigg]\]

上式可以理解为从\(s\)开始智能体按照策略\(\Pi\)来行动并获得一系列回报序列，这些序列效用的期望即为策略\(\Pi\)在状态\(s\)下的效用。

显然最优策略\(\Pi^*\)对于任意状态\(s\)满足：

\[\Pi^* = \arg \max_{\Pi} \mathbb{E} \bigg[ \sum_{t=0}^\infty \gamma^t R(s_t) \bigg\vert \Pi \bigg]\]

它在状态\(s\)下对应的行为需要最大化后续的效用：

\[\Pi^* (s) = \arg \max_{a \in A(s)} \sum_{s'} T(s, a, s') U(s')\]

\(U(s)\)表示按照最优策略\(\Pi^*\)获得的效用，称为真实效用(true utility)，即\(U(s) = U^{\Pi^*}(s)\)。我们把上面的式子结合到一起就得到了最优策略的效用：

\[U(s) = R(s) + \gamma \cdot \max_{a \in A(s)} \sum_{s'} T(s, a, s') U(s')\]

上式是求解MDP问题最重要的方程，称为Bellman方程(Bellman equation)。

Finding Policies

Value Iteration

本节最后的问题是如何来求解Bellman方程。由于Bellman方程是非线性的，我们很难显式地进行求解，一般需要采用迭代的方法：

\[\hat{U}_{t+1}(s) = R(s) + \gamma \cdot \max_{a \in A(s)} \sum_{s'} T(s, a, s') \hat{U}_t(s')\]

式中\(\hat{U}_t(s)\)为\(t\)时刻状态\(s\)的效用。这样的迭代过程称为价值迭代(value iteration)，同时可以证明从任意的效用函数出发，通过价值迭代总可以收敛到真实效用。

Policy Iteration

除了价值迭代外另一种常用的求解方法为策略迭代(policy iteration)。对于任意给定的策略\(\Pi_t\)我们可以利用Bellman方程计算它在\(t\)步的效用：

\[U_t(s) = R(s) + \gamma \sum_{s'} T(s, \Pi_t(s), s') U_t(s')\]

然后我们选择具有最大效用的行为来改进它：

\[\Pi_{t+1} (s) = \arg \max_{a \in A(s)} \sum_{s'} T(s, a, s') U_t(s')\]

如此反复迭代即可得到最优策略。类似于价值迭代，我们同样可以证明无论初始策略如何采用策略迭代一定会收敛到最优策略。