OMSCS-ML课程笔记02-Regression
这个系列是Gatech OMSCS 机器学习课程(CS 7641: Machine Learning)的同步课程笔记。课程内容涉及监督学习、无监督学习和强化学习三个部分,本节主要介绍监督学习中回归问题的相关内容。
Linear Regression
监督学习是利用给定的数据(特征)\(X\)与去预测因变量\(y\),当\(y\)为连续型变量时则称此时的问题是一个回归(regression)问题。对于回归问题最基本的算法是线性回归(linear regression),此时我们假定因变量\(y\)是特征\(X\)的线性组合:
\[y = X_1 \beta_1 + X_2 \beta_2 + \cdots + X_p \beta_p = X \beta\]其中\(\beta\)为组合系数。在某些情况下还需要考虑一个偏置项\(\beta_0\),此时只需要对\(X\)进行増广即可:\(X = [1, X_1, ..., X_p]^T\)。

线性回归的目标是求解出合适的组合系数\(\beta\)使得总体误差最小,最常用的方法是使用最小二乘法(least square)来进行求解,此时的误差为样本预测值与实际值之差的平方和:
\[\text{RSS}(\beta) = \sum_{i=1}^N ( y_i - X_i \beta )^2 = (\mathbf{y} - \mathbf{X} \beta)^T (\mathbf{y} - \mathbf{X} \beta)\]上式说明误差\(\text{RSS}(\beta)\)是关于系数\(\beta\)的二次型。对\(\text{RSS}(\beta)\)求导并令导数为0得到:
\[\mathbf{X}^T (\mathbf{y} - \mathbf{X} \beta) = 0\]求解方程最后得到\(\beta\)的估计值:
\[\hat{\beta} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}\]其中\((\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T\)也称为\(\mathbf{X}\)的伪逆(Moore–Penrose inverse)。
从矩阵的角度上看\(\beta\)实际上是对\(\mathbf{X}\)的列向量进行了线性组合,因此使用最小二乘法的过程也可以理解为将\(\mathbf{y}\)投影到\(\mathbf{X}\)列向量构成的空间中得到正交投影\(\hat{y} = \mathbf{X} \hat{\beta}\)的过程。

Polynomial Regression
在某些情况下因变量\(y\)与特征\(X\)不存在线性关系,此时直接使用线性回归算法不会有比较好的结果,因此需要对样本的特征进行增强。比较常用的做法是引入特征的高次项作为新的特征:
\[y = \beta_0 + X \beta_1 + X^2 \beta_2 + \cdots + X^p \beta_p = X \beta\]我们称此时的回归问题为多项式回归(polynomial regression)。对于多项式回归同样可以按线性回归进行求解,只需要重新构造数据特征矩阵\(\mathbf{X}\)即可。
需要主要的是使用多项式回归时需要对特征的次数\(p\)进行控制:若\(p\)比较小则模型的行为会趋近于一般的线性模型,可能无法处理相对复杂的问题;若\(p\)很大则很容易出现过拟合的现象。实际中一般会结合交叉验证来选择合适的次数。
Cross Validation
本节最后来简单介绍下交叉验证(cross validation)的内容。我们可以把数据集上的样本看做是从某个总体分布中进行抽样的结果,显然我们希望能在已有的数据集上去估计模型在总体分布上的性能。交叉验证提供了通过已有数据估计模型泛化能力的方法,其中比较常用的方法是k-fold交叉验证(k-fold cross-validation):把训练数据随机打乱并均分为k份,然后每次训练选择其中的一份来测试模型性能其他的用来训练,最后不断轮换测试数据并取模型在轮换性能的平均值作为模型的性能。

k-fold交叉验证的一种极端情况是取k为训练数据总数,此时每次只在一个数据点上进行验证并需要对整个数据集进行遍历。称这种交叉验证方法为留一法(leave-one-out cross-validation):
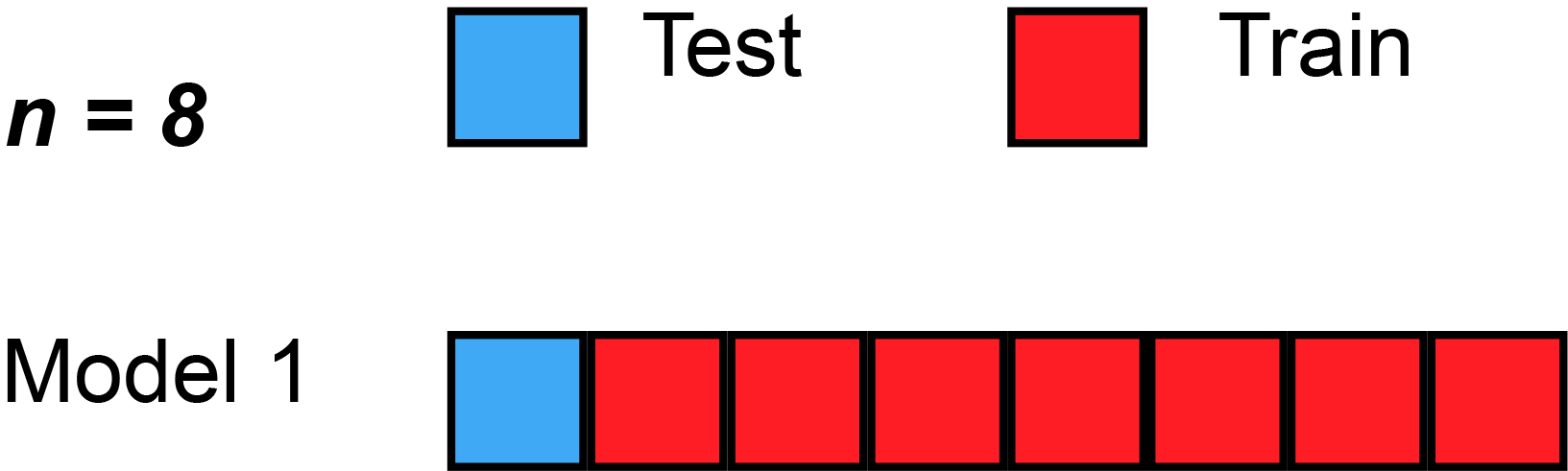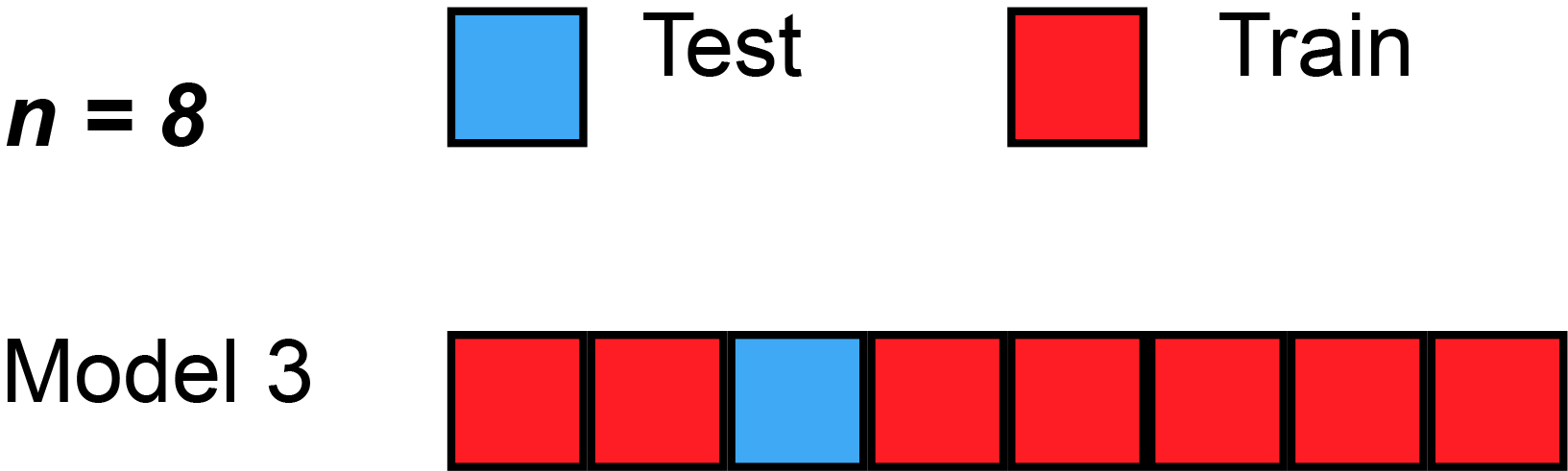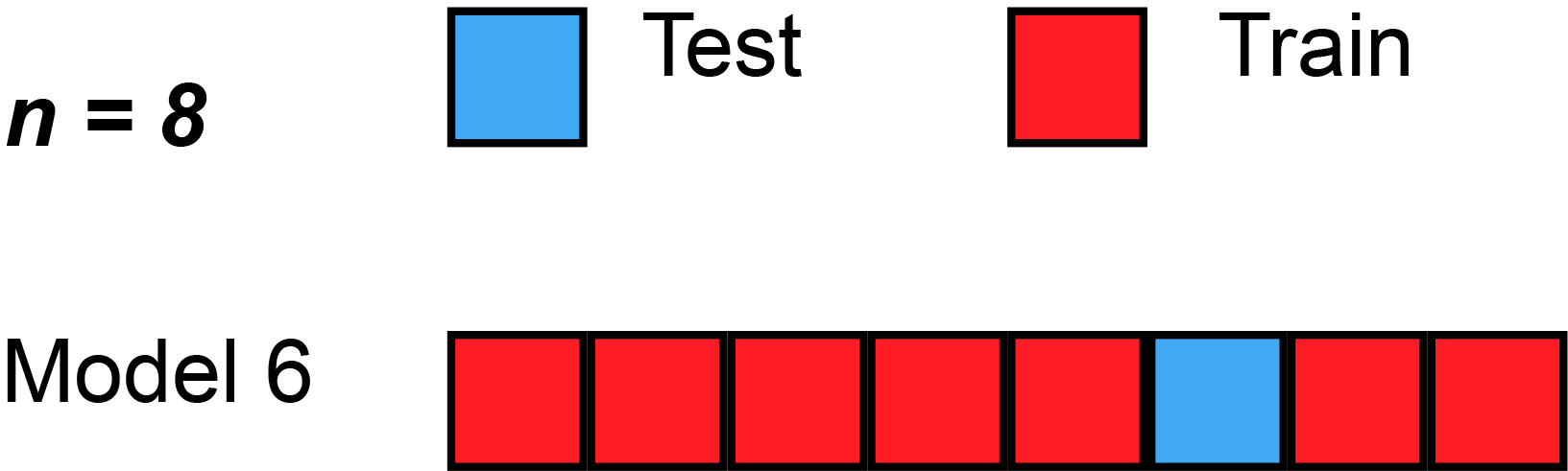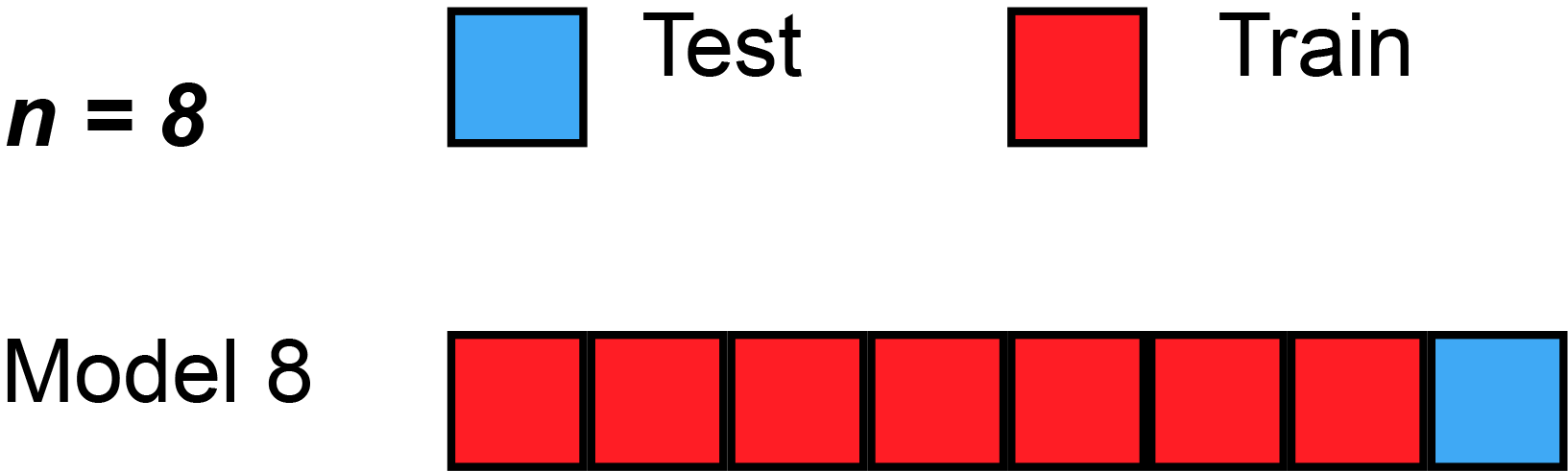
通过交叉验证我们可以从有限的数据中获得尽可能多的有效信息,从而最大限度地利用已有的数据。同时我们可以通过交叉验证来选择模型的超参数从而避免出现过拟合等问题。