深蓝学院-GNN课程笔记04-图神经网络

这个系列是深蓝学院图深度学习理论与实践的同步课程笔记。课程内容涉及图深度学习的基础理论与应用，本节主要介绍图神经网络的相关内容。

图神经网络

在前面的课程中我们介绍过图嵌入的发展过程，包括以数据降维为代表的第一代图嵌入技术以及以word2vec为基础的第二代图嵌入技术，而在本节课中我们将介绍以图神经网络(graph neural network, GNN)为代表的第三代图嵌入技术。

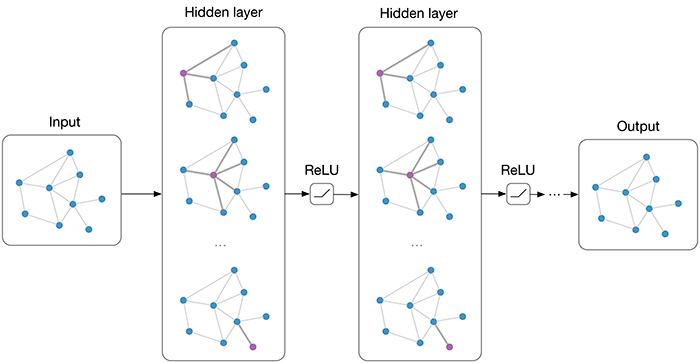
GNN旨在将深度神经网络的相关方法应用到图上。由于图不是规则的数据结构，在GNN中需要一些额外的操作包括侧重于节点的图滤波以及侧重于图整体的图池化。

谱图论

图滤波的基础是谱图论。在前面的课程中我们介绍过拉普拉斯矩阵描述了图上每个节点与它相邻节点之间的差异：

\[h = L f = Df - Af\] \[h_i = \sum_{v_j \in N(v_i)} (f_i - f_j)\] \[f^T L f = \frac{1}{2} \sum_{v_i \in V} \sum_{v_j \in N(v_i)} (f_i - f_j)^2\]

同时拉普拉斯矩阵还描述了图的频域性质，图上的傅里叶变换由拉普拉斯矩阵给出：

\[F = U^T f\] \[f = U F\] \[L = U \Lambda U^T\]

其中\(f\)和\(F\)分别是图信号的空域和频域表示；\(U\)为拉普拉斯矩阵\(L\)的特征向量矩阵；\(\Lambda\)为\(L\)的特征值。由于拉普拉斯矩阵\(L\)是(半)正定对称的，它的特征值为非负数也称为图的频率。

图滤波

图谱滤波

最基本的图滤波方式是基于谱图论的图谱滤波。对于图信号\(f\)我们首先利用图傅里叶变换得到频率：

\[\hat{f} = U^T f\]

\(\hat{f}\)中的每个值表示该信号在不同频率上的相应。我们可以利用一个滤波器来对频率信号进行处理：

\[\hat{g}(\Lambda) = \begin{bmatrix} \hat{g}(\lambda_0) & & & \\ & \hat{g}(\lambda_1) & & \\ & & \ddots & \\ & & & \hat{g}(\lambda_{N-1}) \\ \end{bmatrix}\]

最后利用图逆傅里叶变换来重构图信号：

\[f' = U \hat{g}(\Lambda) U^T f\]

显然图谱滤波的核心是设计滤波器\(\hat{g}(\Lambda)\)，这可以通过训练一个前馈神经网络来从数据中进行学习。然而这种方式的主要缺陷在于它具有过大的计算复杂度：对于包含\(N\)个节点\(d_1\)维信号的图，如果要输出\(d_2\)维数量的信号，模型的参数量为\(N \times d_1 \times d_2\)；同时图谱滤波还需要对图进行特征值分解，这又提高了计算的复杂度。因此图谱滤波很难直接应用到大规模图上。

Chebyshev Filter

为了降低计算复杂度，我们可以利用一个多项式来拟合\(\hat{g}(\Lambda)\)：

\[\hat{g}(\Lambda) = \begin{bmatrix} \sum_k \theta_k \lambda_0^k & & & \\ & \sum_k \theta_k \lambda_1^k & & \\ & & \ddots & \\ & & & \sum_k \theta_k \lambda_{N-1}^k \\ \end{bmatrix}\]

其中参数\(\theta_k\)由不同频率所共享。通过这样定义的滤波器我们还可以避免对图进行特征值分解：

\[U \hat{g}(\Lambda) U^T f = \sum_k \theta_k U \Lambda^k U^T f = \sum_k \theta_k L^k f\]

在工程中更常用的方式是使用Chebyshev多项式来代替标准的多项式，这样使得训练过程更加稳定。Chebyshev多项式可以通过递归来定义：

\[T_0 (x) = 1, T_1(x) = x\] \[T_k (x) = 2x T_{k-1}(x) - T_{k-2}(x)\]

由于Chebyshev多项式是定义在区间[-1, 1]上的，在使用它进行滤波时首先需要对频率进行缩放：

\[\tilde \lambda_i = \frac{2 \lambda_i}{\lambda_{\max}} - 1\]

这样使用Chebyshev多项式进行图谱滤波可以表示为：

\[U \hat{g}(\Lambda) U^T f = \sum_k \theta_k T_k(\tilde L) f\] \[\tilde L = \frac{2 L}{\lambda_{\max}} - I\]

与传统图谱滤波相比使用Chebyshev多项式作为滤波器具有更少的参数、训练时无需矩阵特征值分解、同时训练过程也更加稳定。

GCN

在GCN中我们进一步只考虑一阶的Chebyshev多项式，同时假设\(\lambda_{\max} = 2\)：

\[\hat{g}(\Lambda) = \theta_0 + \theta_1 (\Lambda - I)\]

更进一步假设\(\theta = \theta_0 = -\theta_1\)：

\[\hat{g}(\Lambda) = \theta (2I - \Lambda)\] \[U \hat{g}(\Lambda) U^T f = \theta (2I - L) f = \theta (I + D^{-\frac{1}{2}} A D^{-\frac{1}{2}}) f\]

令\(\tilde{A} = I + A\)并进行规范化就得到了GCN滤波器的最终形式：

\[U \hat{g}(\Lambda) U^T f = \theta (\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}) f\] \[\tilde{D}_{ii} = \sum_j \tilde{A}_{ij}\]

对于包含多通道的图信号我们则需要将所有输入通道整合起来，此时的滤波过程可以表示为：

\[F' = (\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}) F \Theta\]

其中\(\Theta\)为卷积的参数矩阵。

记\(\hat{A} = \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}\)，那么图滤波的过程也可以表示为：

\[F' = \hat{A} F \Theta\]

对于给定的节点\(v_i\)，滤波后的结果为：

\[F'_i = \sum_j \hat{A}_{ij} F_j \Theta\]

注意到\(\hat{A}_{ij}\)仅在节点\(v_i\)和\(v_j\)不相连时取0，因此GCN在空域上可以理解为将每个节点所有相邻的节点的信息收集到一起然后进行特征变换得到最后的输出信息。

\[F'_i = \sum_j \hat{A}_{ij} F_j \Theta = \sum_{v_j \in N(v_i) \cup \{v_i\}} \hat{A}_{ij} F_j \Theta\]

图空域滤波

现代图神经网络大多是基于图空域滤波来实现的。类似于空域视角下的GCN，图空域滤波可以理解为图上每个节点收集了相邻节点的信息并重新整合得到新的信息。如GraphSage中每个节点从它的邻域中采样\(S\)个节点，然后利用一个聚合函数AGG来实现信息整合：

\[N_S(v_i) = \text{SAMPLE}(N(v_i), S)\] \[f_{N_S(v_i)}' = \text{AGG}(\{ F_j \vert \forall v_j \in N_S(v_i) \})\] \[F'_i = \sigma( [F_i, f_{N_S(v_i)}'] \Theta)\]

聚合函数AGG可以选择求和、求平均甚至是LSTM等。

GAT则利用注意力机制为每个相邻节点的信息赋予了权重：

\[F'_i = \sum_{v_j \in N(v_i) \cup \{v_i\}} \alpha_{ij} F_j \Theta\] \[\alpha_{ij} = \frac{\exp \bigg( \text{LeakyReLU} (a^T [F_i \Theta, F_j \Theta]) \bigg)}{\sum_{v_k \in N(v_i) \cup \{v_i\}} \exp \bigg( \text{LeakyReLU} (a^T [F_i \Theta, F_k \Theta]) \bigg)}\]

当图上存在边的信息时还可以利用该信息来设计滤波器。如ECC为不同类型的边设计了相应类型的参数矩阵：

\[F'_i = \frac{1}{N(v_i)} \sum_{v_j \in N(v_i)} F_j \Theta_{\text{tp}(v_i, v_j)}\]

其中\(\Theta_{\text{tp}(v_i, v_j)}\)表示类型为\(\text{tp}(v_i, v_j)\)的边所共享的参数矩阵。

GGNN还提出使用GRU来整合邻域的信息：

\[m_i = \sum_{(v_j, v_i) \in E} \Theta_{\text{tp}(v_i, v_j)} F_j\] \[F_i' = \text{GRU} (m_i, F_i)\]

PPNP提出了使用Personalized PageRank来进行消息传播，GCN、GraphSage和GAT都可以看成是PPNP的特例：

\[F'_i = \sum_{v_j \in V} P_{ij} F_j \Theta\] \[P = \beta (I - (1 - \beta) \hat{A})^{-1}\]

\(P_{ij}\)表示从\(v_i\)出发进行随机游走到\(v_j\)的概率。

为了克服PPNP计算复杂、可拓展性差的缺陷，APPNP提出使用迭代的方式来逼近\(F'\)。相应的迭代公式为：

\[F_{out}^{(k)} = (1 - \beta) \hat{A} F_{out}^{(k-1)} + \beta F \Theta\]

可以证明当\(k \to \infty\)时，APPNP会收敛到PPNP。

图信号降噪

从图信号降噪的角度我们可以将上述所有的图神经网络同一到一个框架中。记原始图信号为\(F\)，经过特征变换后为\(F_{\text{tr}} = F \Theta\)，我们可以定义如下的图信号降噪问题：

\[\begin{aligned} \arg \min_{F'} L(F') &= \Vert F' - F_{\text{tr}} \Vert_F^2 + c \cdot \frac{1}{2} \sum_{i \in V} \frac{1}{\vert N(i) \vert} \sum_{j \in N(i)} \Vert F_i' - F_j' \Vert_2^2 \\ &= \Vert F' - F_{\text{tr}} \Vert_F^2 + c \cdot \text{tr} (F'^T L F') \end{aligned}\]

其中第一项\(\Vert F' - F_{\text{tr}} \Vert_F^2\)要求降噪后的信号与原始输入信号足够接近，而第二项\(\text{tr} (F'^T L F')\)则要求降噪后每个节点的信号与它的邻域信号足够接近，常数\(c\)控制了两项损失之间的比例。

我们对\(L(F')\)求导并令导数为0可以得到最优的输出信号\(F'\)：

\[\frac{\partial L}{\partial F'} = 2 (F' - F_{\text{tr}}) + 2c \cdot L F' = 0\] \[F' = (I + c L)^{-1} F_{\text{tr}} = (I + c (I - \hat{A}))^{-1} F_{\text{tr}} = \frac{1}{1+c} (I - \frac{c}{1+c} \hat{A})^{-1} F_{\text{tr}}\]

进一步令\(\beta = \frac{1}{1+c}\)，我们就可以得到PPNP的更新公式：

\[F' = P F_{\text{tr}}\] \[P = \beta (I - (1 - \beta) \hat{A})^{-1}\]

如果我们使用梯度下降来求解这个图降噪问题，则可以建立迭代公式：

\[F' \leftarrow F' - b \cdot \frac{\partial L}{\partial F'}\]

在\(F' = F_{\text{tr}}\)处的导数为：

\[\frac{\partial L}{\partial F'} \bigg\vert_{F' = F_{\text{tr}}} = 2c \cdot L F_{\text{tr}}\]

进行一步迭代可以得到：

\[F' = F_{\text{tr}} - 2 bc L F_{\text{tr}} = (1 - 2 bc) F_{\text{tr}} + 2 bc \hat{A} F_{\text{tr}}\]

令\(2bc = 1\)就得到了GCN的更新公式：

\[F' = \hat{A} F_{\text{tr}}\]

如果我们假设降噪后每个节点与它邻域的相似度不同，则可以将优化目标修改为：

\[\arg \min_{F'} L(F') = \Vert F' - F_{\text{tr}} \Vert_F^2 + \frac{1}{2} \sum_{i \in V} c_i \cdot \frac{1}{\vert N(i) \vert} \sum_{v_j \in N(i)} \Vert F_i' - F_j' \Vert_2^2\]

对节点\(v_i\)求偏导得到：

\[\frac{\partial L}{\partial F'[i, :]} = 2 (F'[i, :] - F_{\text{tr}}[i, :]) + \sum_{v_j \in N(v_i)} (c_i + c_j) \cdot (F'[i, :] - F'[j, :])\]

还是在\(F' = F_{\text{tr}}\)处使用梯度下降进行求解，进行一次迭代得到：

\[F'[i, :] = \bigg( 1 - b \sum_{v_j \in N(v_i)} (c_i + c_j) \bigg) F_{\text{tr}}[i, :] + \sum_{v_j \in N(v_i)} b (c_i + c_j) F_{\text{tr}}[j, :]\]

令\(b \sum_{v_j \in N(v_i)} (c_i + c_j) = 1\)则可以得到GAT的更新公式：

\[F'[i, :] = \sum_{v_j \in N(v_i)} b (c_i + c_j) F_{\text{tr}}[j, :] = \sum_{v_j \in N(v_i)} \alpha_{ij} F_{\text{tr}}[j, :]\]

最后，我们把它们统一起来用同一个优化问题来表达：

\[\arg \min_{F'} L(F') = \Vert F' - F_{\text{tr}} \Vert_F^2 + R(F')\]

其中\(R(F')\)表示图信号的先验，对于GCN和PPNP可以取

\[R(F') = c \cdot \frac{1}{2} \sum_{i \in V} \frac{1}{\vert N(i) \vert} \sum_{j \in N(i)} \Vert F_i' - F_j' \Vert_2^2\]

而对于GAT则可以取

\[R(F') = \frac{1}{2} \sum_{i \in V} c_i \cdot \frac{1}{\vert N(i) \vert} \sum_{v_j \in N(i)} \Vert F_i' - F_j' \Vert_2^2\]

对于不同类型的图神经网络，我们相当于选择相应的先验和求解方法来求解同一个降噪问题。

图池化

图池化是GNN中另一种重要的操作。类似于CNN中池化层对数据进行降维，我们可以利用图池化来缩减图的规模。

平面图池化

最基本的图池化方法是平面图池化，我们把整张图缩减到一个节点。常用的平面图池化包括均值池化或是最大值池化。

我们还可以在图上插入一个虚拟节点来进行池化。此时这个虚拟节点与图上的所有其他节点相连，然后在这个新图上训练一个GNN来获得节点嵌入。这个虚拟节点的嵌入即可作为原来整张图的池化结果。

除此之外，我们还可以把注意力机制引入到图池化中。此时我们需要为图上的每个节点计算一个注意力分数\(s_i\)，然后将所有节点的嵌入加权求和作为最终的池化结果。

层次图池化

平面图池化的一个局限在于池化后我们失去了图的结构信息，而在层次图池化中我们则是通过逐步的粗池化直到获得图的表示，因此可以保留不同层次下图的结构信息。

gPool是层次图池化的经典方法，它的思想是在图上选择一部分比较重要的节点来构造新图从而完成图池化。在选择节点时gPool使用了节点重要性分数\(y\)来度量节点的重要性，并从中选择得分最高的\(n_p\)个节点以及对应邻接矩阵的行和列作为备用节点特征。最终池化后的节点特征等于原始节点特征与重要性分数经过sigmoid函数的乘积：

SAGPool的流程与gPool基本一致，但在计算重要性得分时使用了一个GCN来完成计算：

另一种层次图池化的方法是使用一个GNN来生成子图。在DiffPool中使用了2个GCN模型，其中一个用来生成分配矩阵\(S\)而另一个用来生成备用节点特征\(F_\text{inter}\)：

最后将这两个矩阵结合起来即可获得池化后的新图：

DiffPool在空域中进行池化，而EigenPool则是在谱域进行聚类从而实现图池化。EigenPool首先需要在图上进行谱聚类，从而得到一系列互不重叠的簇作为粗化图的超节点并利用这些超节点构造出新图\(A_p\)。

接着我们在每个子图上进行图傅里叶变换得到相应的傅里叶系数作为新图上节点的嵌入。一般情况下我们可以只保留每个子图上的前\(K\)个系数作为截断的傅里叶系数，这样既能保证变换后仍然保留了大部分原始的信号同时还能降低计算的复杂度。